De toestand

Nu en dan komen we een bericht tegen, waarin gewag wordt gemaakt van klimaatverandering in Nederland, en waarbij vermeld wordt dat rond 1987 een temperatuursprong heeft plaatsgevonden. Over klimaatverandering zijn vrijwel alle onderzoekers het wel eens, maar een sprong? Dat impliceert een vrij abrupte overgang van een ‘oud’ klimaat naar een ‘nieuw’ klimaat.
Hieronder een grafiek met jaarlijkse temperaturen. Voor de verandering deze keer eens niet van De Bilt, maar de zogeheten Centraal Nederland Temperatuur reeks (over 1907 t/m 2011), samengesteld uit meerdere stations in midden Nederland.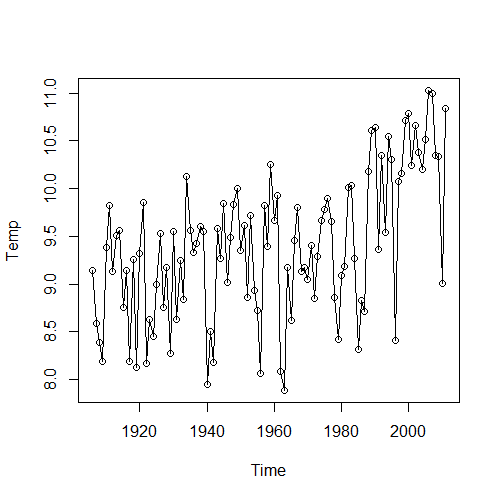
In een dergelijke grafiek is slechts met grote moeite enige trend te zien, de jaarlijkse variaties (tot 2 graden) overheersen. Gelukkig zijn er een aantal statistische hulpmiddelen om een beter overzicht te krijgen.

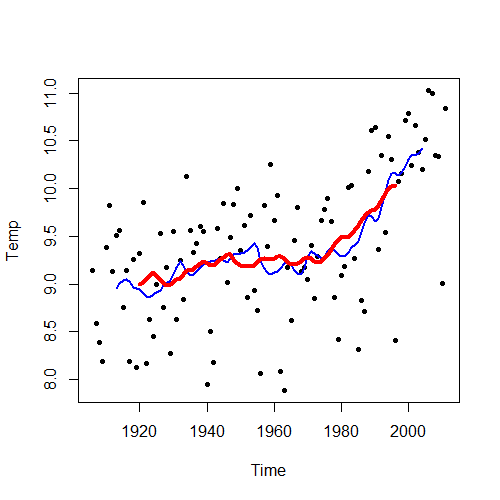
Allereerst kunnen we de zeer grote fluctuaties wat minder maken door gemiddelden over meerdere jaren weer te geven, bijvoorbeeld lopende gemiddelden over 15 respectievelijk 30 jaar. Als we spreken over klimaat, worden vaak gegevens over 30 jaar genomen.
Een temperatuurstijging is nu onmiskenbaar aanwezig. Wel valt op dat de stijging niet erg gelijkmatig plaatsvindt: in de laatste decennia is de stijging een stuk groter dan eerder.
Het grote nadeel van dergelijke langlopende gemiddelden is, dat de jaren aan de beide uiteinden veel minder meetellen dan andere jaren.

Hoeveel de temperatuur gemiddeld over alle jaren is veranderd, kunnen we zien door een lineaire trend weer te geven. Opnieuw is er een duidelijk positieve trend, met daaromheen voortdurend waarden aan de plus- en minkant van die trendlijn. De lineaire trend bedraagt +0,13°C/10jr over de jaren 1907-2011, en is zeer significant.

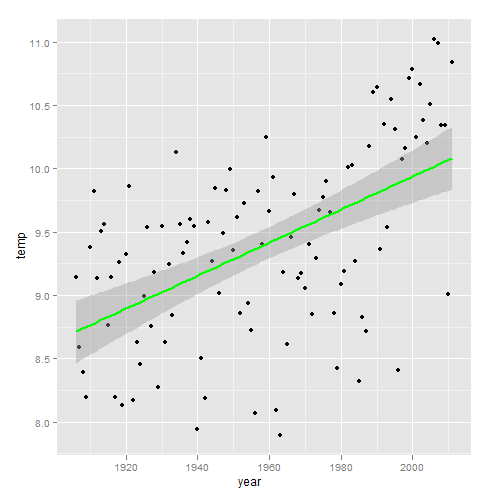
De grote fluctuaties rondom de trendlijn laten al zien dat de trend geen ideale manier is om alle gegevens samen te vatten. Het toont wel duidelijk dat de temperatuur heden ten dage ruim een graad hoger ligt in Nederland dan zo’n 100 jaar geleden. Maar zo’n lineaire trend suggereert (de aard van het beestje) een gemiddeld gelijkmatige stijging, terwijl een eerdere grafiek al liet zien dat de temperatuurstijging de laatste decennia groter is dan eerder.
Er zou sprake kunnen zijn van een trendbreuk, dat wil zeggen dat de trend in een eerdere periode anders is dan later. Er zijn diverse statistische methoden om zoiets te onderzoeken.
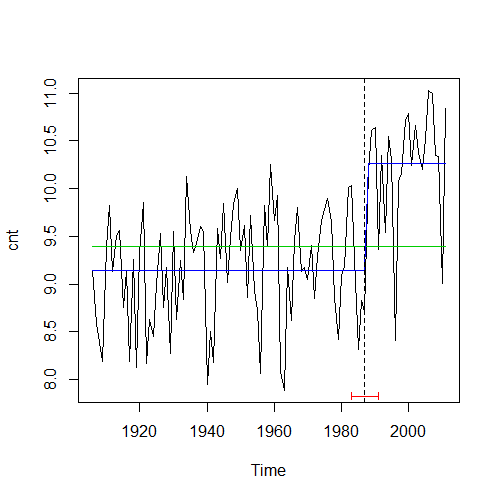Met een Chow test vinden we een significant breekpunt rond het jaar 1987 (functie Fstats in de strucchange library van R) . Met een andere test uit hetzelfde pakket vinden we eveneens 1987 (functie breakpoints). De groene lijn toont het gemiddelde over alle jaren, de blauwe lijn de gemiddelden voor en na het breekpunt. De gemiddelden tonen een ‘sprong’ van 9,1° naar 10,3°.
De afgebeelde gemiddelden zeggen in werkelijkheid echter niet zoveel. In de grafiek hieronder hebben we die vervangen door lineaire trendlijnen voor en na het breekpunt van 1987.
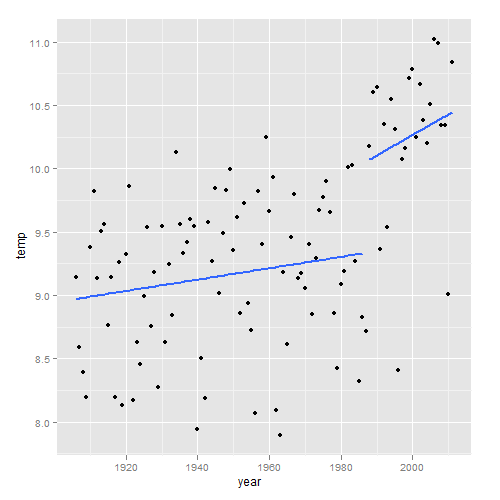We zien nu een sprong omhoog plus een steilere trend na 1987.
Nader onderzoek laat zien dat het jaar 1987 niet altijd naar boven komt, als we apart de maanden bekijken (de breekpunten via de functies Fstat / breakpoints):
januari: 1987  / geen
februari: 1987 / geen
maart: 1988 / 1988
april: 1992 / 1992
mei: 1987 / 1987
juni: 1929 / 1929
juli: 1981 / 1981
augustus: 1988 / 1988
september: 1925 / 1925
oktober: 1952 / geen
november: 1925 / 1925
december: 1970 / geen

We zien dat 1987 (of 1988) vijf keer uit de bus komt via de F-stat methode (en zeven keer een ander jaar). Via de breakpoint methode komt 1987 (of 1988) slechts drie keer naar voren (vijf keer een ander jaar, en vier keer helemaal geen breekpunt). Van eenduidigheid over het jaar 1987 is absoluut geen sprake.

De boven getoonde grafiek toont eigenlijk een breekpunt in combinatie met een sprong. Niet alleen verandert de trend rond het breekpunt, de trend maakt ook nog eens een sprong.
Via een andere methode (de segmented library in R) kunnen we een breekpunt opsporen zonder een sprong, waarbij het eind van de ene trend overgaat in het begin van de andere trend. We vinden opnieuw een breekpunt, maar nu echter in het jaar 1980.
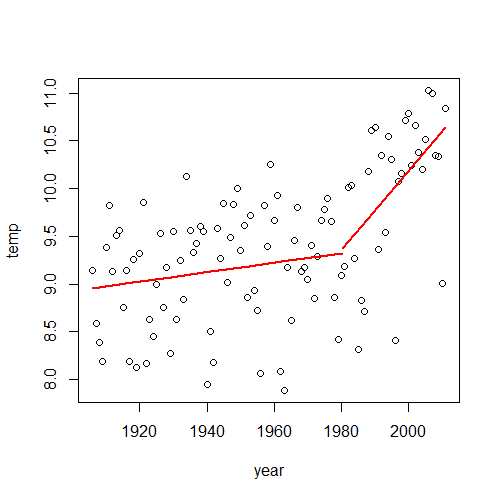Inherent aan methodieken om een breekpunt op te sporen, is dat bij sterk fluctuerende tijdreeksen al snel wel ergens een breekpunt gevonden wordt. De belangrijkste vraag moet dan direct zijn: is er een fysieke oorzaak aan te wijzen? Over het jaar 1987 als mogelijk breekpunt in het Nederlandse klimaat zijn in het verleden diverse artikelen verschenen in onder meer Weerspiegel en Meteorologica, maar een bevredigend antwoord op de vraag naar een fysieke oorzaak is bij mijn weten nooit naar boven gekomen.

Als we niet willen uitgaan van een gelijkmatige trend over de tijdreeks, niet proberen ergens een ‘simpele’ sprong of breuk te vinden, en ook (in tegenstelling tot een langjarig gemiddelde) alle gegevens even veel waarde willen geven, is er dan een methode die ons aanschouwelijk kan maken hoe de temperatuur in Nederland in grote lijnen is veranderd? Jawel, een veel gebruikte methode is loess, waarvan het resultaat hieronder is afgebeeld. Net als in de meeste hierboven gebruikte methodes zien we ook nu een sterkere stijging de laatste decennia dan eerder, echter zonder een of ander breekpunt.
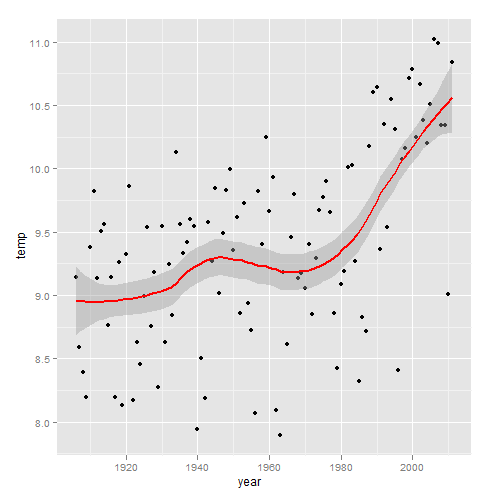Elk van de bovengenoemde statistische methodes probeert uit de ruwe gegevens een ‘model’ te maken waarbij een dusdanig lijn wordt geconstrueerd, dat het verschil tussen de ruwe waarden en de lijn minimaal is. Maar welk model benadert nu het meest de werkelijkheid? Daarvoor kunnen we het Akaike Information Criterion (AIC) bepalen. Des te lager de AIC waarde, des te beter het model de ruwe gegevens benadert. We vinden dan:

– lineair model: AIC 211
– breakpoints model: AIC 195
– segmented model: AIC 202
– loess model: AIC 40

Het loess model heeft overduidelijk een veel betere AIC dan de andere modellen, en is in dit geval te prefereren. Merk op dat AIC geen absolute, alleen een relatieve betekenis heeft. Het is dus niet zo dat in algemene zin een AIC boven de 100 ‘slecht’ is of onder de 50 ‘goed’. Het kan enkel gebruikt worden om voor eenzelfde tijdreeks te bepalen welk model beter of slechter een samenvatting geeft van de ruwe data.

Dat hier het loess model de voorkeur krijgt, wil niet zeggen dat de andere modellen waardeloos zijn. Het lineaire model laat zien dat over de gehele periode 1907-2011 er een gemiddelde opwarming in centraal Nederland was van 0,13°C per 10 jaar. Zowel het breakpoints als het segmented model tonen dat de opwarming de laatste decennia een stuk sterker is dan daarvoor.

We verwerpen echter het idee van een sprong in de temperatuur dat vastgepind zou kunnen worden op een bepaald jaar. Statistisch onderzoek naar een sprong is enkel zinvol als verondersteld kan worden dat er een fysieke oorzaak is die mogelijk een sprongsgewijs gevolg kan hebben. Lukraak gaan zoeken naar mogelijke sprongen is even zinloos als lukraak gaan zoeken naar mogelijke cycli in reeksen. Wie genoeg zoekt zal altijd wel iets kunnen vinden.
Lezenswaardig in dit verband zijn enkele artikelen op het blog Open Mind: “Steps“, “Step 2” en “Step 3“.

Een ding hebben alle vermelde statistische modellen gemeen: ze kunnen niet gebruikt worden om even een simpele prognose te maken voor de komende jaren of decennia. Klimaatprognoses worden niet gemaakt middels het ‘doortrekken van wat lijnen’, zoals wel eens beweerd wordt.

Wat wel vaststaat is, dat ook in Nederland sprake is van een klimaatverandering die onder meer zichtbaar is in de temperaturen. Die verandering is niet vast te pinnen op een bepaald jaar. Het volstrekt zich ook niet als een continu geleidelijk proces. Het gaat ‘met horten en stoten’, soms een paar jaar de ene kant op, dan weer een jaar de andere kant op.
Zoals één zwaluw nog geen zomer maakt, net zomin maakt één koel jaar zoals 2010 een eind aan een trend van stijgende temperaturen. Er is geen ‘sprong’ gemaakt naar een nieuw klimaat dat nu min of meer stabiel blijft. Klimaatverandering gaat nog wel even door, ook in Nederland.